| Jūs esate čia: Pradžia » Visos temos » Mokslas » Matematika |
|
Pradėkime nuo skaitiklio arba viršutinės trupmenos dalies. Tokiu būdu rasime tris laipsnius – su ta pačia baze, bet skirtingais laipsnio rodikliais. Šios užduoties tikslas – pasiekti situaciją, kai didžiausias laipsnis išliktų toks pat kaip ir mažiausias, bet su daugybos simboliu. Būtų didelė klaida pačioje pradžioje sutrumpinti tuos pačius du laipsnius, nes tai skirtingi matematiniai veiksmai (sudėtis ir dalyba). Taigi, pradėkime nuo 5 pakėlimo 12-uoju laipsniu. Kaip tai padaryti? Ištraukdami skaičių iš skliaustų, turime prisiminti, kad visi skliaustų elementai, padauginti iš jo, turi duoti tą patį rezultatą kaip ir pradžioje. Pirmojo komponento atveju jis bus tiesiog 1. Toliau jis bus 5 pakelta 1-uoju laipsniu, nes 5 pakelti 13-uoju laipsniu galima užrašyti kaip 5 pakelti 12-uoju laipsniu, padauginus iš 5 pakeltu 1-uoju laipsniu. Tuo pačiu pagrindu pašaliname paskutinį komponentą, todėl skliausteliuose lieka 5 pakelta 2-uoju laipsniu. Skaičių 5 galime pakelti 12-uoju laipsniu, kuris yra ir skaitiklyje, ir vardiklyje, taigi lieka 1 + 5 pakelti 1-uoju laipsniu + 5 pakelti 2-uoju laipsniu, t. y. 1 + 5 + 25 = 31. Tai yra teisingas šio matematikos galvosūkio sprendimas.
MTPC parengtą informaciją atgaminti visuomenės informavimo priemonėse bei interneto tinklalapiuose be raštiško VšĮ „Mokslo ir technologijų populiarinimo centras“ sutikimo draudžiama.
|



 (
(
 (
(

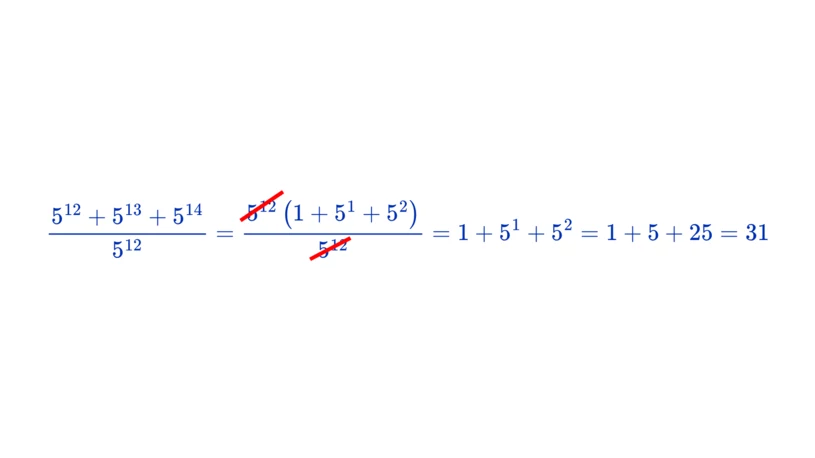




 104
104 (3)
(3)
.png)



.png)













